What does it mean when a student gets a correct answer in math? Are they all set, do they know the material? Does it matter how they got that answer?

This post will quickly explore those questions with all the great information we gather at Math ANEX. The answer isn’t as simple as we’d hope, because learning isn’t as simple as we like to think it is.

How Likely Is It That A Student Can Get The Right Answer Again, Given That They Got It Before?

The answer to the question above is 10.4, or something equivalent. 52/5 is another popular choice by students. But if you get this question right, and then you take a year of algebra. How likely are you to get it right again? We like to think that it’s 100%. We’ve solved that, so learning has been achieved and we can move on to the next topic. Or have we?

In fact, in this example of several thousand students, we see that a little under 80% of students get the right answer twice in a row. And an incorrect answer of 9.6 (if you accidentally subtract 4 from the right side instead of add), is almost as likely to change into the right answer as it is for a student to get it right two times in a row.

When we think about student’s performing, we like to think that if they get it right, they will always get it right. But that just isn’t the case.

However, there may be some ways to better predict how well a student understands the topic and whether or not it will stick with them.

Let’s take a look at a different problem.

To get the right answer, you need to first find the difference between the stack of two pots and four pots to get the height of two pot lips (32-24=8cm). Then divide that by 2 to get the height of the lip of one pot (8/2=4cm). Then we can subtract one pot lid from the height of 2 pots and get the height of one pot. (24 – 4 = 20cm).

Students who write a full explanation, like the above, show us that they know what is happening. Does that matter? Does it make a difference if they can clearly articulate what is happening vs. if they say, “I used math to get my answer.”?

The answer is yes.

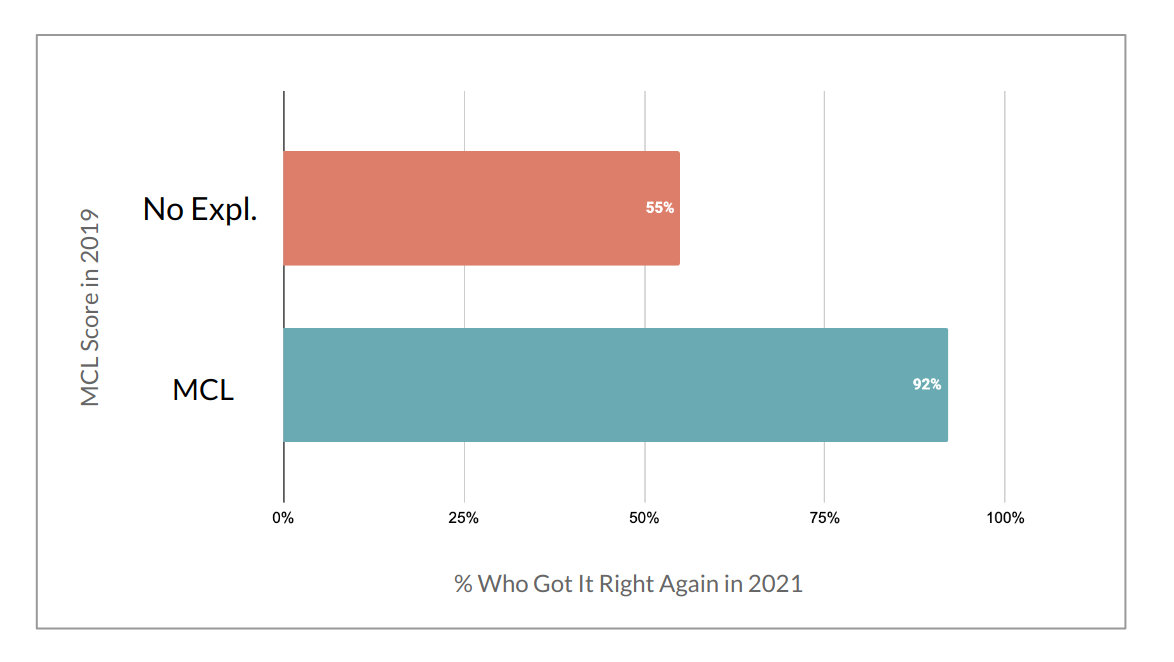
If we look at how well students communicated across their communication of the mathematics involved (M), connection to the context of the problems including units and key topics (C) and the reasoning and logic behind the mathematics (L), we see a significant difference in the prediction of how well students will do in the future. Students who clearly articulated why they got their answer had a 92% chance of getting the right answer 3 years later. Whereas only 55% of students who wrote no explanation, or something like “I don’t know”, got the right answer again.

And I won’t dive deeply into how I think about incorrect answers in this post, but students who show good reasoning in how they think about an incorrect answer are also more likely to get the wrong answer again in the future.

Communication matters. What else matters?

The way students solve a problem matters

Let’s use the problem above to consider why it matters how students solve a problem. One way to solve this problem is to first take the cost of the bike and subtract what Raul already has in the bank. (340-60=$280). Then divide that by the amount that Raul earns per day to get the number of days Raul needs to work to buy the bike. (280/20 = 14 days).

Some students use linear equations: 20x + 60 = 340.

Others Divide Like I Did: (340 – 60)/20 = 14.

Others “Multiply and Check”: 20 x 20 = 400. Too much, 20 x 13 = 260. Close. 20 x 14 = 280.

Others Repeat Subtract: 280 – 20 – 20 – 20 – 20… And then count the 20s.

Some Repeat Add: 60 + 20 + 20 + 20 + 20… And then count the 20s.

And some count up. 60,80,100,120,140, etc. And count the steps.

As you would imagine, some of these are easier than others and some are more error prone than others.

In a sample of the students in 8th grade that counted up or used repeated addition, ~50% got a D or an F in Algebra 1 their next year. And they got the question right. But unfortunately, if you haven’t started utilizing higher level tools before algebra, the class is just going to be harder.

We used this analysis on a similar problem and this is what we saw.

While it is a low chance that students use some of these outdated tools, it’s important to understand how students are solving problems because even if they get it right, the way they do it matters, and if we can deeply understand how they are thinking about problems and what tools they are using, we can provide the right help to make sure they excel in math.

If you want to get to talk about how this work is done or other ways we think about asset-based assessments, get in touch or check us out on twitter.