We have the incredibly fortunate opportunity to be working with a group of 7 amazing Integrated Math 1 teachers this school year. These teachers, to no surprise, care deeply about helping their students improve and they’re open to finding brand new ways to do so. They’re allowing us to try out weekly asset-based classwork assignments. These assignments will be designed to help make it easier to improve student learning, while also pushing us to be top notch in our analysis of student mathematical thinking.

This post is a brief look at our work in the first section of Integrated Math 1. We will do a weekly post as we navigate and discover all the ways students approach IM-1 concepts and learn the skills they need to be successful. Let’s dive in!

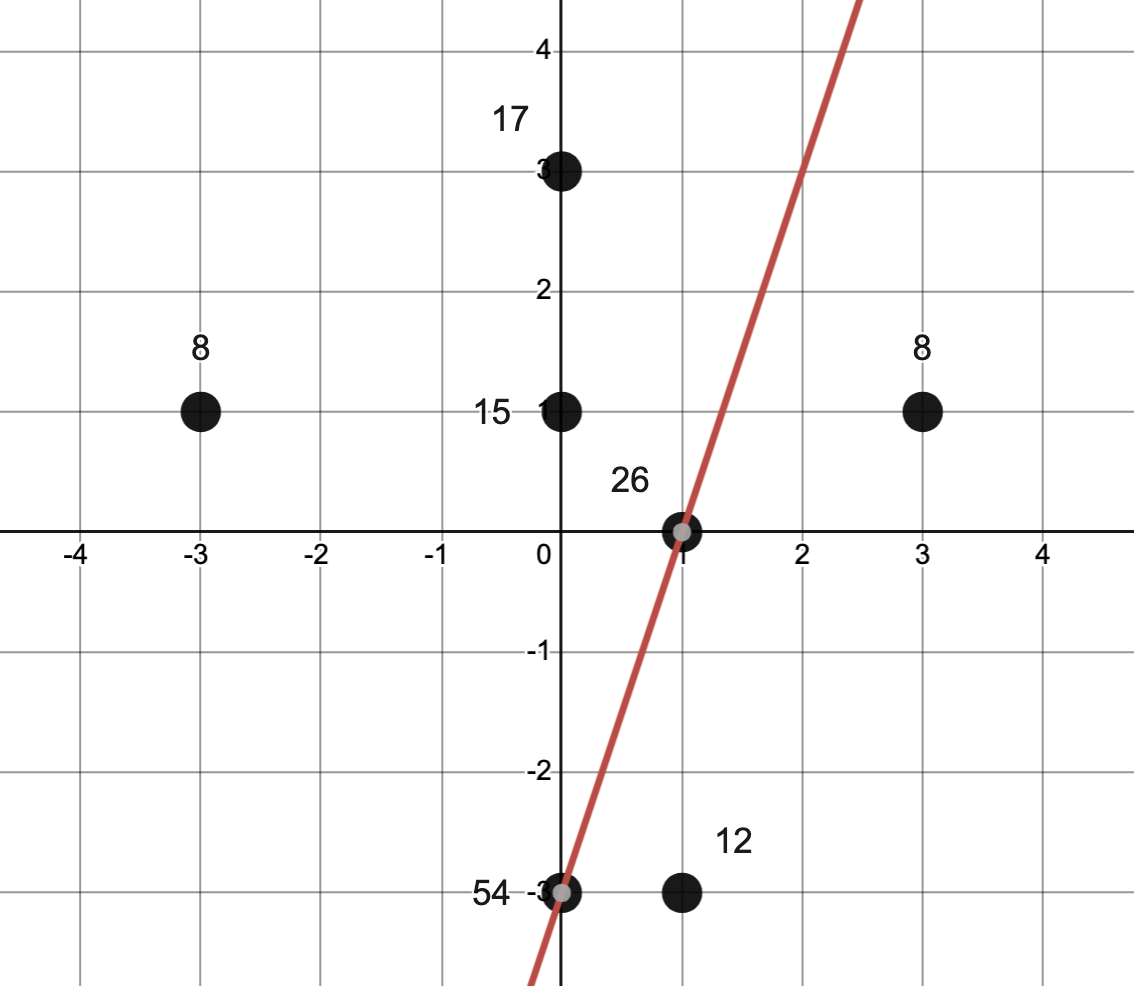
Question 1: Coordinates, Graphs, and Y-Intercepts.

Given the graph below, what is the coordinate point of the y-intercept?

This question is intended as a ramp question, something relatively easy to get things started. However, we quickly saw a variety of answers. We are working with about 450 students and here were the top 5 answers.

Student Answer	% of Students (# of Students)
-3	29% (132)
(0, -3)	12% (54)
1	8% (37)
3	8% (35)
(1, 0)	6% (26)

As you can see, we have a variety of answers, representing about 60% of the class in the top 5 answers.

-3 being the value of y at the y-intercept, but not in coordinate form

(0, -3) being the correct coordinate

1 being the value of x at the x-intercept

3 being the distance of y-value from 0 (or the slope, an unfortunate mistake on our part)

(1, 0) being the correct coordinates of the x-intercept

We even made a graph to represent the top coordinate pairs that students wrote. The numeric labels of each point are how many students wrote that as their point. You’ll notice that everyone one of them is some combination of the x and y intercepts (the numbers 0, 1, and 3.)

And that is really cool. All of these students, while many not getting it quite correct, are indeed on track. With some re-engagement, I would bet that we would see them be able to make that leap to “fully correct” very quickly. These points, and the answers not in coordinate point form (ex. -3), represent more than 3/4ths of the students at this school.

Plus, this leads to a great re-engagement activity that anyone could use with their class. The idea is to work with the students to figure out why someone might write a different coordinate pair and what they could do in the future to remember to write the right one.

We have prepared a teacher facing and student facing guide to work through these if you would like to use them in your own classroom.

So what happened a week later after the teachers re-engaged students with the above exercises? We had to find out, so we gave a graph with a different line, and here were the results:

First, we see a big jump in students getting the correct coordinates, which is awesome. And then partial evidence (which is essentially mixed up x,y pairs, giving the negative of the y intercept, etc.) and an increase in incomplete evidence (which are any cases where we aren’t seeing any evidence of the y-intercept). While these comparisons are great, we also like to look at matched pair students and see which category they were in last week compared to this week.

We see a couple of key things here. Students who got the correct coordinates last time, generally got them again. Then we see huge gains for partial evidence, but also some losses. This information encourages us to go and potentially talk to some of the students who showed less evidence of understanding. How did they think about the question last time? And how did they think about it this time? What changed and where did they get lost in the last week? That will open up a dialogue to help identify where they are struggling. This really allows us to dive in to the complexity of learning. It is a journey with many ups and downs.

Question Group 2: Pattern Recognition and Translating It Into An Equation

Every year a deer sheds its antlers and then regrows a larger set the next year. A 3 year old deer has antlers with 7 points as seen in the picture above. 

Question 1:  Predict how many points the deer’s antlers will have when it is 5 years old. 

Question 2:  Explain your process for how you got your answer for the problem above. 

Question 3: Write a function that models deer age in years (x) and number of antler points (y) in the form y = mx + b. 

In question 1, we saw a couple mistakes, like predicting for year 4 instead of year 5. But 90% of the students had 1 of 3 patterns.

Growing by 2 year over year

Growing by 3 year over year because the first year it went from 0 at 0 years to 3 at 1 year

Growing by 7 year over year because “a 3 year old deer has antlers with 7 points”.

The beautiful part is that they don’t come out of nowhere.

Other answers we see from the explanations come from ideas like 7/3 = 2.33, so 2.33 antlers per year, etc. And some students guess and estimate. Almost all students are seeing the patterns.

However, jumping to question 3, we see a big hurdle in translating this pattern into an equation. Let’s even segment this down and just look at the students who found the pattern of growing by 2.

Slope	% of Students (# of Students)	Possible Reason
2	37.5% (130)	Correct Slope
Plugged in for x instead of m	25% (88)	You plug in values for x not m
3	10% (36)	Growth from 0 years to 1 year or first value of antlers.
1	10% (34)	Just default x + …
5	4% (15)	Antlers in year 2

And the intercept.

Intercept	% of Students (# of Students)	Possible Reason
2	25% (87)	Growth Rate is 2
1	20% (72)	2 + 1 = 3 for year 1
3	19% (65)	Year 1 as x = 0.
b	11.5% (40)	Didn’t know what to do with + b
Did not include Intercept	9% (31)	Didn’t know what to do with + b

There is a lot to go through here, but the first thing that jumps out at me is that a lot of students aren’t sure how patterns translate into equations. They are using the numbers they have at their disposal, but aren’t reasoning through how it all fits together. Given that so many students could identify the pattern, we’d hope to see that translate into getting at least the slope right. But instead, we actually see more getting a proper starting value (b value or y-intercept).

The good news is that we can leverage this information. If they can plug the numbers into a formula and check, they can start to see the relationship. And once again, we can practice to make it go smoothly next time.

We prepared some practice material here as well.
Teacher Facing
Student Facing

One quick thing though. In the last paragraph, I do believe that having them plug into a formula to check would work for many of the students IF they are decent with simple equations. Luckily, we can check that assumption! (And I do later in the post)

But for now, let’s see how students improved over a week and after a re-engagement exercise.

We immediately can see huge gains in getting the right equation and getting the slope. That’s a huge improvement from just a week ago, and incredible for setting up the foundation for a successful Integrated 1/Algebra 1 course.

Let’s look at the students more closely.

Here we see some small losses from everywhere in not getting this equation at all. But mostly we see a ton of gains across the board. We still have lots of work to do in getting many students more comfortable writing equations, but you can also tell there is a lot of struggle when it comes to using the y-intercept in an equation, even though we saw solid gains in identifying the intercept on a graph.

We will keep exploring this topic in future assessments and see how we can get students more comfortable. I am very curious to see what equations they would write for a graph and see if that might help show us how we can bring some of these concepts together for them.

Question Group 3: Solving Equations

In this group, we were looking for students ability to solve and simplify equations.

Question 1: Solve for x. 2x – 1 = -33

Question 2: Solve for y. -7(3y + 8) – 9 = 40

Question 3: Simplify the following 6xy + 5x + 12 + 7y + 2x + 13 + 3xy – 1y

Instead of covering all 3, I am going to dive into Question 1 since it related to how useful it might be to students using equations to double check their work on writing equations for patterns.

Top answers for 2x – 1 = -33.

Value of X	% of Students (# of Students)	Possible Way To Get Answer
-16	47% (213)	Correct answer
16	7% (33)	Forget the negative sign
-17	6% (28)	Move the -1 over instead of adding 1 to both sides
17	6% (27)	Move the -1 over and forget about the negative

2/3 of students fall into what I would say are very simple mistakes. Take away the negatives and a make it even more simple and I would say most students would be able to check their equation with the pattern!

Other students didn’t divide by the 2 in 2x, and there were other several small mistakes, but students did generally seem to understand what they were asked to do.

Looking across the other equations, what we decided to do was to put students in different categories for solving equations. Evidence of Strength, Evidence of Proficiency, or Incomplete Evidence. And what we could do with that is help forgive some small mistakes. For example, if you got 16 on the first one but -5 for -7(3y + 8) – 9 = 40, then we could forgive the small mistake in missing the negative on the first one.

We believe that we all make small mistakes and they shouldn’t be counted against you. By figuring out how you can get all the incorrect answers, you can better understand what small mistakes are being made, if they are consistent, and whether or not to take action.

For example, 10% of the students who got 16 and forgot the negative on the first one, got the next two correct. That seems like a small mistake/accident to me and we are happy to forgive it. However, the 16% who got 16 and then 5, both times forgetting the negative, may need to be asked about how they are solving the questions in more detail.

This was a brief overview of what we learned about the students’ ways of thinking after the first week. Next week, we are doing some repeat questions to see if we were able to make improvements after the re-engagement lessons.

If this work sounds like something you’d want to have for your district, school or students. Contact Us or DM Us On Twitter.

Or check out the next post in the series about how students think about function notation.